PROVING TRIGONOMETRIC IDENTITIES EXAMPLES

Example 1 :

Prove the following identities.

(i) sec⁴θ (1 - sin⁴θ) - 2tan²θ  =  1

Solution :

sec⁴θ (1 - sin⁴θ) - 2tan²θ :

   =   sec⁴θ [(1²)² - (sin²θ)²] - 2tan²θ

   =   sec⁴θ [(1 + sin²θ) (1 - sin²θ)] - 2tan²θ

   =   (1/cos⁴θ)[(1 + sin²θ) cos²θ] - 2tan²θ

   =   [(1 + sin²θ)/cos²θ] - 2tan²θ

   =   (1/cos²θ)  + (sin²θ/cos²θ) - 2tan²θ

   =   sec²θ  + tan²θ - 2tan²θ

   =   sec²θ  - tan²θ

   =  1

Hence proved.

(ii)  (cot θ-cos θ)/(cot θ+cos θ) = (cosec θ-1)/(cosec θ+1)

Solution :

(cot θ - cos θ)/(cot θ + cos θ) : 

  =  ((cos θ/sin θ) - cos θ) / ((cos θ/sin θ) + cos θ) 

  =  ((cos θ-sin θ cos θ)/sin θ) / (cos θ + sin θ cos θ)/sin θ)

  =  ((cos θ-sin θ cos θ) / (cos θ + sin θ cos θ)

  =  cos θ(1 - sin θ) / cos θ(1 + sin θ)

  =  (1 - sin θ)/(1 + sin θ)

  =  [1 - (1/cosec θ)] / [1 + (1/cosec θ)]

  =  (cosec θ - 1) / (cosec θ + 1)

Hence proved.

Example 2 :

Prove the following identities.

(i) [(sin A -  sin B)/(cos A + cos B)]  + [(cos A - cos B)/sin A + sin B)]  =  0

Solution :

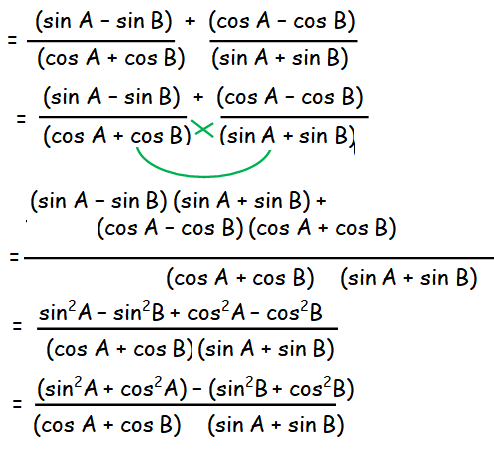
  =  (1 - 1)/(cos A + cos B) (sin A + sin B)

  =  0

Hence proved.

(ii) [(sin³A + cos³A)/(sin A + cos A)] + [(sin³A - cos³A)/(sin A - cos A)]  =  2

Solution :

[(sin³A + cos³A)/(sin A + cos A)] + [(sin³A - cos³A)/(sin A - cos A)] 

a³ + b³  =  (a + b)(a² - ab + b²)

a³ - b³  =  (a - b)(a² + ab + b²)

[(sin³A + cos³A)/(sin A + cos A)]

=  (sin A+cos A)(sin²A+cos²A-sinAcosA)/(sinA+cosA)

=  (sin²A + cos²A - sin A cos A)

=  (1 - sin A cos A)  -------(1)

[(sin³A - cos³A)/(sin A - cos A)]

=  (sin A-cos A)(sin²A+cos²A+sinAcosA)/(sinA-cosA)

=  (sin²A + cos²A + sin A cos A)

=  (1 + sin A cos A)  -------(2)

(1) + (2)

=  1 - sin A cos A + 1 + sin A cos A

=  2

Hence proved.

Example 3 :

(i) If sin θ + cos θ  =  √3 , then prove that

tan θ + cot θ  =  1

Solution :

Given : sin θ + cos θ  =  √3. 

(sin θ + cos θ)²  =  3

sin²θ + cos²θ + 2sin θ cos θ  =  3

2sin θ cos θ  =  3 - 1

sin θ cos θ  =  1

tan θ + cot θ :   

=  (sin θ/cos θ) + (cos θ/sin θ)

=  (sin² θ + cos²θ)/(sin θ cos θ)

=  1/(sin θ cos θ)

=  1/1  

=  1 R.H.S

Hence proved.

(ii) If √3 sin θ − cos θ  =  0, then show that

tan 3θ  =  (3 tan θ - tan³θ)/(1 - 3tan²θ)

Solution :

Given : √3 sin θ − cos θ = 0.

Then,

√3 sin θ = cos θ

sin θ/cos θ  =  1/√3

tan θ  =  1/√3

θ  =  30°

tan 3θ :

=  tan 3(30°)

=  tan 90°

=  undefined -----(1)

(3 tan θ - tan³θ)/(1 - 3tan²θ) :

=  (3tan 30° - tan³30°) / (1 - 3tan²30°)

=  [3(1/√3) - (1/√3)³] / [1 - 3(1/√3)²)]

=  [√3 - (1/3√3)] / [1 - 3(1/3)]

=  [√3 - (1/3√3)] / [1 - 1]

=  [√3 - (1/3√3)] / 0

=  undefined -----(2)

From (1) and (2), we get

tan 3θ  =  (3 tan θ - tan³θ)/(1 - 3tan²θ)

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.