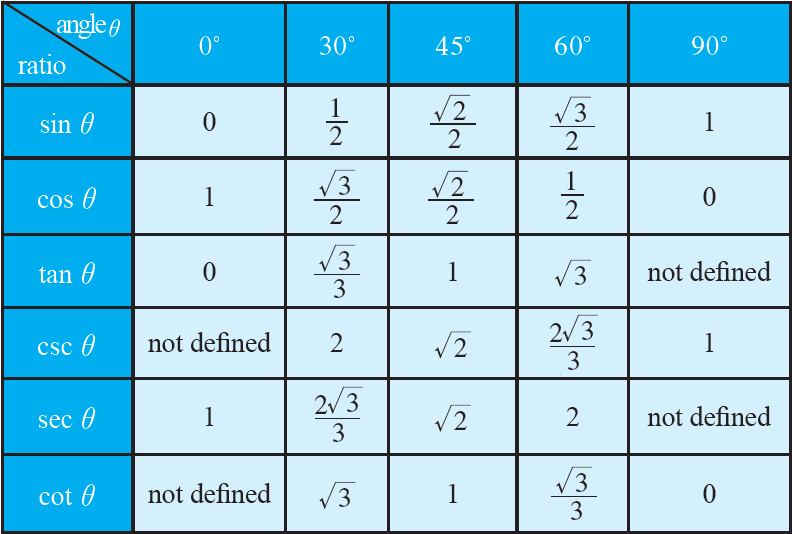
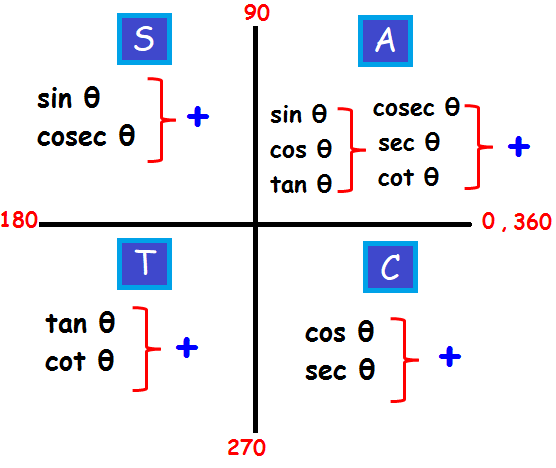
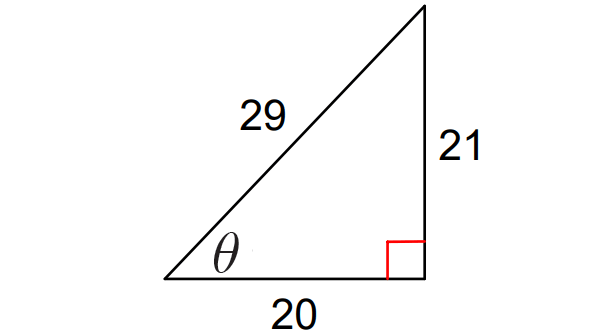
COMPOSITE FUNCTION
In general, suppose that f and g are two functions and that x is a number in the domain of g. By evaluating g at x, we get g(x). If g(x) is in the domain of f, then we may evaluate f at g(x) and obtain the result f[g(x)].
The correspondence from x to f[g(x)] is called a composite function f ∘ g.
Given two functions f and g, the composition function, denoted by f ∘ g (read as "f composed with g"), is defined by
(f ∘ g)(x) = f[g(x)]
The domain of f ∘ g is the set of all numbers x in the domain of g such that g(x) is in the domain of f.
Look at the picture carefully (shown below). Only those x's in the domain of g for which g(x) is in the domain of f can be in the domain of f ∘ g. The reason is that if g(x) is not in the domain of f then f[g(x)] is not defined. Because of this, the domain of f ∘ g is a subset of the domain of g; the range of f ∘ g is a subset of the range of f.
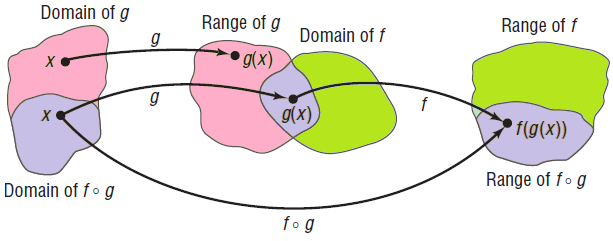
The picture shown below provides a second illustration of the definition. Here x is the input to the function g, yielding g(x). Then g(x) is the input to the function f, yielding f[g(x)]. Notice that the "inside" function g in f[g(x)] is done first.

Example 1 :
Let f(x) = 3x + 2 and g(x) = 5x. Find (f ∘ g) and (g ∘ f).
Solution :
f ∘ g :
f ∘ g = f[g(x)]
= f(5x)
= 3(5x) + 2
= 15x + 2
g ∘ f :
g ∘ f = g[f(x)]
= g(3x + 2)
= 5(3x + 2)
= 15x + 10
Example 2 :
Let f(x) = 2x2 - 3 and g(x) = 4x. Find (f ∘ g) and (g ∘ f).
Solution :
f ∘ g :
f ∘ g = f[g(x)]
= f(4x)
= 2(4x)2 - 3
= 2(42x2) - 3
= 2(16x2) - 3
= 32x2 - 3
g ∘ f :
g ∘ f = g[f(x)]
= g(2x2 - 3)
= 4(2x2 - 3)
= 8x2 - 12
Example 3 :
Let f(x) = x + 3 and g(x) = x2 - 9. Find (f ∘ g) and (g ∘ f).
Solution :
f ∘ g :
f ∘ g = f[g(x)]
= f(x2 - 9)
= (x2 - 9) + 3
= x2 - 9 + 3
= x2 - 6
g ∘ f :
g ∘ f = g[f(x)]
= g(x + 3)
= (x + 3)2 - 9
= (x + 3)(x + 3) - 9
= x2 + 3x + 3x + 9 - 9
= x2 + 6x
Example 4 :
Let f(x) = log10x and g(x) = 10x. Find (f ∘ g) and (g ∘ f).
Solution :
f ∘ g :
f ∘ g = f[g(x)]
= f(10x)
= log1010x
= xlog1010
= x(1)
= x
g ∘ f :
g ∘ f = g[f(x)]
= g(log10x)
= 10log10x
= x
Here f ∘ g = g ∘ f = x.
So f(x) and g(x) are inverse to each other.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Trigonometry Sum and Difference Identities
May 07, 24 09:17 AM
Trigonometry Sum and Difference Identities - Concept - Solved Problems -
Trigonometry Even and Odd Iidentities
May 05, 24 12:25 AM
Trigonometry Even and Odd Iidentities -
SOHCAHTOA Worksheet
May 03, 24 08:50 PM
SOHCAHTOA Worksheet