ISOSCELES EQUILATERAL AND RIGHT TRIANGLES

Isosceles Triangle :

A triangle is isosceles, if it has at least two congruent sides or two congruent angles.

Equilateral Triangle :

A triangle is equilateral, if all the three sides are congruent or all the three angles are congruent.

Right Triangle :

A triangle is right triangle, if one of the angles is right angle (90°).

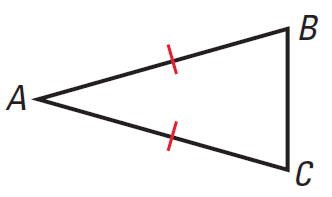
Base Angles Theorem

If two sides of a triangle are congruent, then the angles opposite them are congruent.

If AB ≅ AC, then ∠B ≅ ∠C

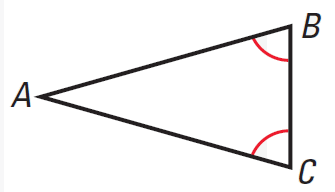
Converse of the Base Angles Theorem

If two sides of a triangle are congruent, then the angles opposite them are congruent.

If ∠B ≅ ∠C, then AB ≅ AC

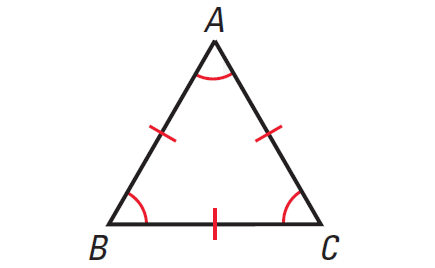
Corollaries to the Above Theorems 

Corollary (i) :

If a triangle is equilateral, then it is equiangular.

Corollary (ii) :

If a triangle is equiangular, then it is equilateral.

The above two corollaries have been illustrated in the picture given below.

Hypotenuse-Leg Congruence Theorem

If the hypotenuse and a leg of a right triangle are congruent to the hypotenuse and a leg of a another right triangle, then the two triangles are congruent.

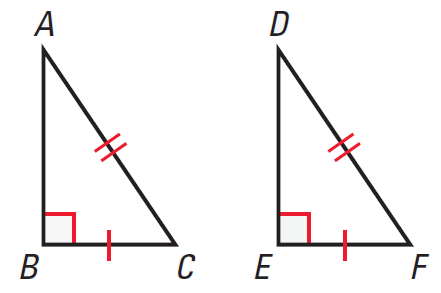
If BC ≅ EF and AC ≅ DF, then ΔABC ≅ ΔDEF.

Solving Problems on Isosceles Equilateral and Right Triangles

Problem 1 :

Use the diagram of ΔABC shown below to prove the Base Angles Theorem.

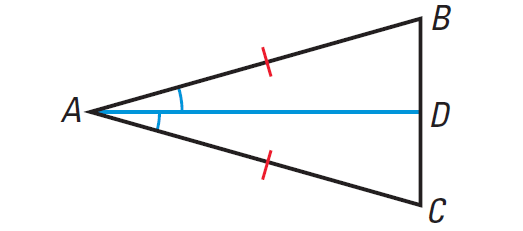
Solution :

Given : In ΔABC, AB ≅ AC.

To prove : ∠B ≅ ∠C.

Proof :

(i) Draw the bisector of ∠CAB.

(ii) By construction, ∠CAD ≅ ∠BAD.

(iii) We are given that AB ≅ AC. Also DA ≅ DA, by the Reflexive Property of Congruence.

(iii) Use the SAS Congruence Postulate to conclude that ΔADB ≅ ΔADC.

(iv) Because corresponding parts of congruent triangles are congruent, it follows that ∠B ≅ ∠C.

Problem 2 :

In the diagram shown below,

(i) find the value of x

(ii) find the value of y

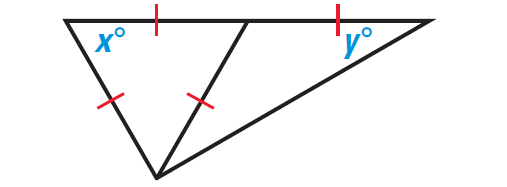
Solution (i) :

In the diagram shown above, x represents the measure of an angle of an equilateral triangle.

From the corollary given above, if a triangle is equilateral, then it is equiangular.

So, the measure of each angle in the equilateral triangle is x.

By the Triangle Sum Theorem, we have

x° + x° + x° = 180°

Simplify. 

3x = 180

Divide both sides by 3 to solve for x.

x = 60

Solution (ii) :

In the diagram shown above, 'y' represents the measure of a base angle of an isosceles triangle.

From the Base Angles Theorem, the other base angle has the same measure. The vertex angle forms a linear pair with a 60° angle, so its measure is 120°.

It has been illustrated in the diagram given below.

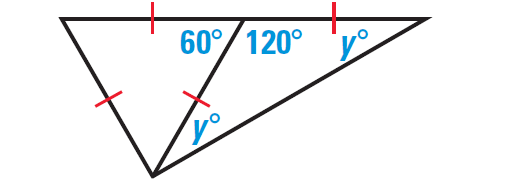
By the Triangle Sum Theorem, we have

120° + y° + y° = 180°

Simplify.

120 + 2y = 180

Subtract 120 from both sides.

2y = 60

Divide both sides by 2.

y = 30

Problem 3 :

The television antenna is perpendicular to the plane containing the points B. C, D and E. Each of the stays running from the top of the antenna to B, C, and D uses the same length of cable. Prove that  ΔAEB, ΔAEC and ΔAED are congruent.

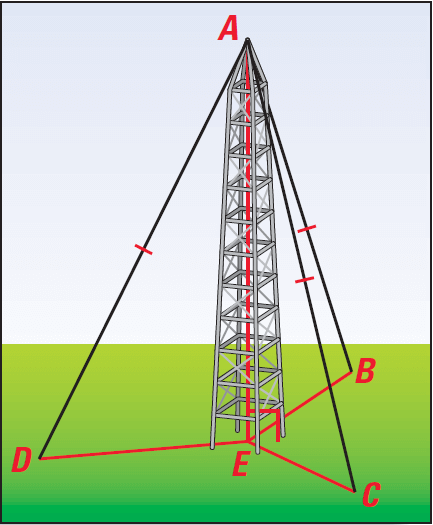
Solution :

Given : AE ⊥ EB, AE ⊥ EC, AE ⊥ ED,  AB ≅ AC ≅ AD.

To Prove : ΔAEB ≅ ΔAEC ≅ ΔAED.

Proof :

(i) We are given that AE ⊥ EB and AE ⊥ EC which implies that ∠AEB ≅ ∠AEC are right angles.

(ii) By definition, ΔAEB and and ΔAEC are right triangles.

(iii) We are given that the hypotenuse of these two triangles AB and AC are congruent.

(iv) Also, AE is a leg for both the triangles and AE ≅ AE by the Reflexive Property of Congruence. Thus, by the Hypotenuse-Leg Congruence Theorem,  ΔAEB ≅ ΔAEC.

(v) Similar reasoning can be used to prove that ΔAEC ≅ ΔAED. So, by the Transitive Property of Congruent Triangles, ΔAEB ≅ ΔAEC ≅ ΔAED.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.