UNIT CIRCLE WORKSHEET

Problem 1 :

Show that the point A(4/5, -3/5) is on the unit circle.

Problem 2 :

Show that the point P(√3/3, √6/3) is on the unit circle.

Problem 3 :

The point P is on the unit circle. Find P(x, y) from the given information. The y-coordinate of P is -1/3 and the x-coordinate is positive.

Problem 4 :

If the the point P(√3/2, k) is on the unit circle in quadrant IV, find the value of k.

Problem 5 :

The point P is on the unit circle. Find P(x, y) from the given information. The x-coordinate of P is -2/5 and P lies above the x-axis.

Problem 6 :

The point P is on the unit circle. Find P(x, y) from the given information. The y-coordinate of P is -1/2 and P lies on the left side of y-axis.

Problems 7-12 : Find the terminal point on the unit circle determined by each real number t.

Problem 7 :

t = 3π

Problem 8 :

t = -π

Problem 9 :

t = -π/2

Problem 10 :

t = -π/4

Problem 11 :

t = 3π/4

Problem 12 :

t = -5π/6

Problems 13-16 : Find the reference number for each value of t.

Problem 13 :

t = 5π/6

Problem 14 :

t = 7π/4

Problem 15 :

t = -2π/3

Problem 16 :

t = 5.80

Problems 17-20 : Find the terminal point on the unit circle determined by each real number t.

Problem 17 :

t = 5π/6

Problem 18 :

t = 7π/4

Problem 19 :

t = -2π/3

Problem 20 :

t = 29π/6

Answers

1. Answer :

We have to show that this point satisfies the equation of the unit circle, that is, x² + y² = 1.

(4/5)² + (-3/5)² = 16/25 + 9/25

= (16 + 9)/25

= 25/25

= 1

So, A is on the unit circle.

2. Answer :

We have to show that this point satisfies the equation of the unit circle, that is, x² + y² = 1.

(√3/3)² + (√6/3)² = 3/9 + 6/9

= (3 + 6)/9

= 9/9

= 1

So, P is on the unit circle.

3. Answer :

Because the point is on the unit circle, we have

x² + (-1/3)² = 1

x² + 1/9 = 1

Subtract 1/9 from each side.

x² = 1 - 1/9

x² = 9/9 - 1/9

x² = (9 - 1)/9

x² = 8/9

Take square root on both sides.

x = ±2√2/3

Because x-coordinate is negative,

x = 2√2/3

The point is

P(2√2/3, -1/3)

4. Answer :

Because the point is on the unit circle, we have

(√3/2)² + k² = 1

3/4 + k² = 1

Subtract 3/4 from both sides.

k² = 1 - 3/4

k² = 4/4 - 3/4

k² = (4 - 3)/4

k² = 1/4

Take square root on both sides.

k = ±1/2

Because the point is in quadrant IV and k is the y-coordinate, the value of k must be negative.

So, k = -1/2.

5. Answer :

Because the point is on the unit circle, we have

(-2/5)² + y² = 1

4/25 + y² = 1

Subtract 4/25 from each side.

y² = 1 - 4/25

y² = 25/25 - 4/25

y² = (25 - 4)/25

y² = 21/25

Take square root on both sides.

y = ±√21/5

Because P lies above the x-axis, y-coordinate must be positive.

y = √21/5

The point is

P(-2/5, √21/5)

6. Answer :

Because the point is on the unit circle, we have

x² + (-1/2)² = 1

x² + 1/4 = 1

Subtract 1/4 from each side.

x² = 1 - 1/4

x² = 4/4 - 1/4

x² = (4 - 1)/4

x² = 3/4

Take square root on both sides.

x = ±√3/2

Because P lies on the left side of y-axis, x-coordinate must be negative.

x = -√3/2

The point is

P(-√3/2, -1/2)

7. Answer :

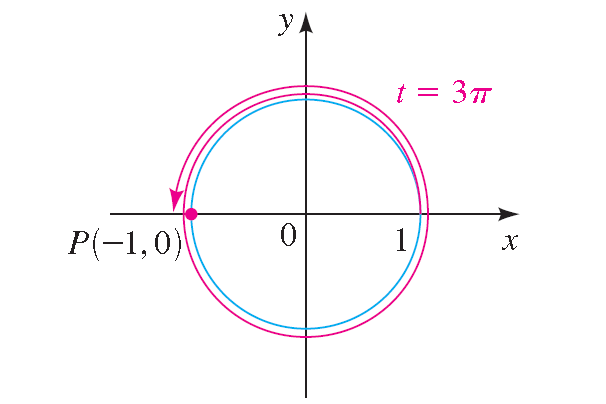
The terminal point determined by 3π is (-1, -0).

8. Answer :

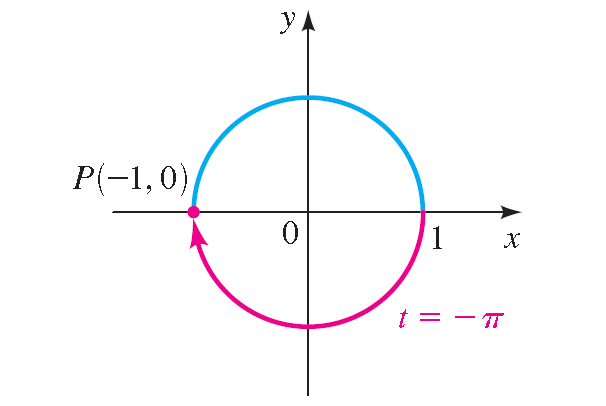
The terminal point determined by -π is (-1, -0).

9. Answer :

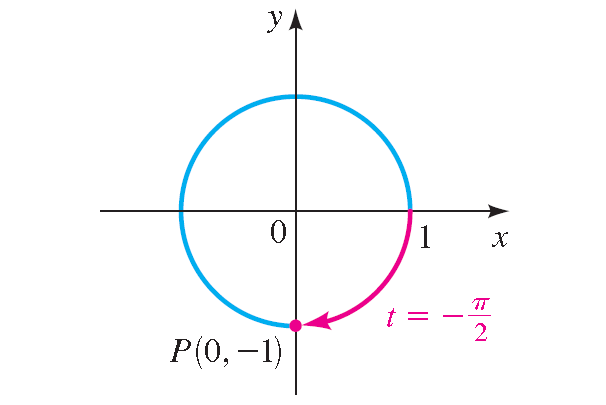
The terminal point determined by -π/2 is (0, -1).

10. Answer :

Let P be the terminal point determined by -π/4, and let Q be the terminal point determined by π/4. In the diagram shown below, we see that the point P has the same coordinates as Q except for sign.

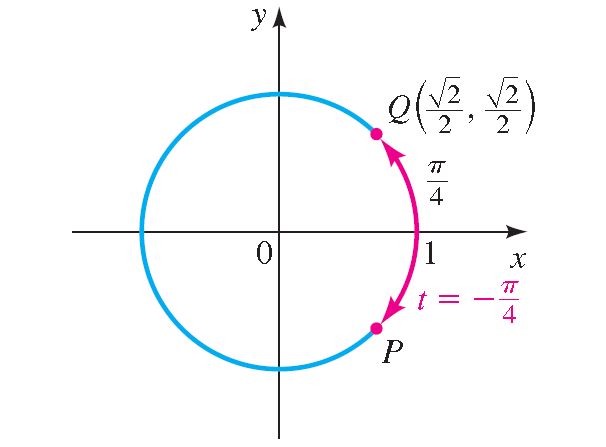
Because P is in quadrant IV, its x-coordinate is positive and its y-coordinate is negative. Thus, the terminal point is

P(√2/2, -√2/2)

11. Answer :

Let P be the terminal point determined by 3π/4, and let Q be the terminal point determined by π/4. In the diagram shown below, we see that the point P has the same coordinates as Q except for sign.

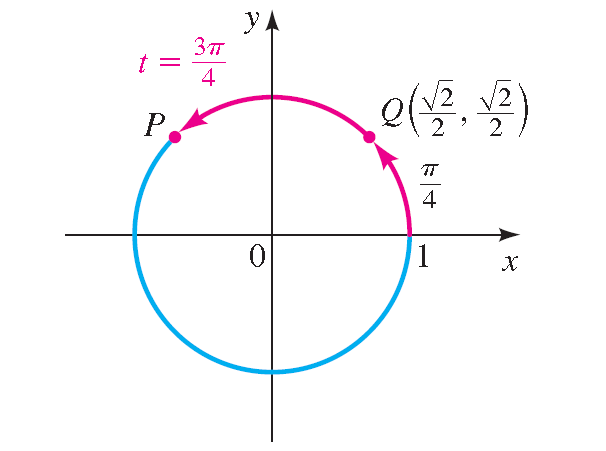
Because P is in quadrant II, its x-coordinate is negative and its y-coordinate is positive. Thus, the terminal point is

P(-√2/2, √2/2)

12. Answer :

Let P be the terminal point determined by -5π/6, and let Q be the terminal point determined by π/6. In the diagram shown below, we see that the point P has the same coordinates as Q except for sign.

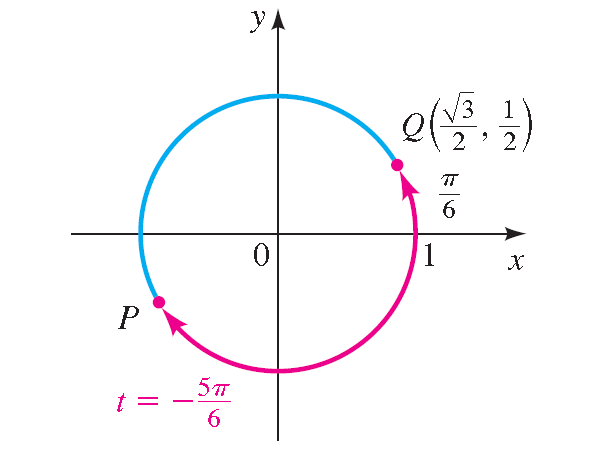
Because P is in quadrant III, its both x-coordinate and y-coordinate are negative. Thus, the terminal point is

P(-√3/2, -1/2)

13. Answer :

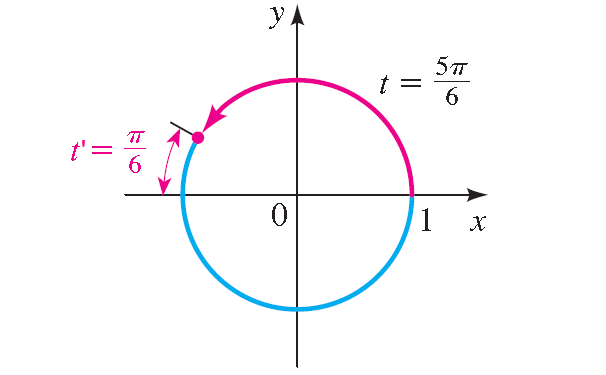
t' = π - 5π/6 = π/6

14. Answer :

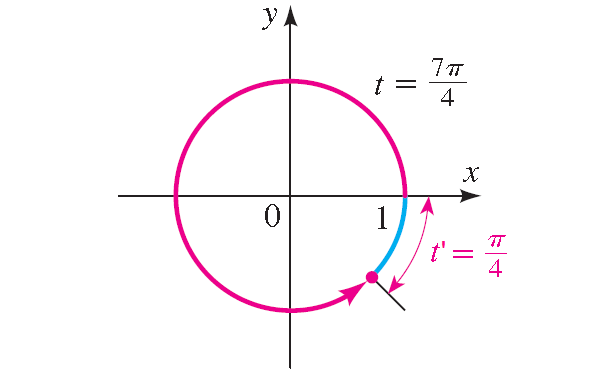
t' = 2π - 7π/4 = π/4

15. Answer :

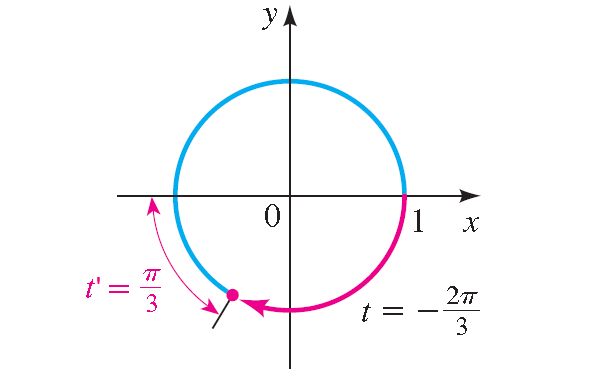
t' = π - 2π/3 = π/3

16. Answer :

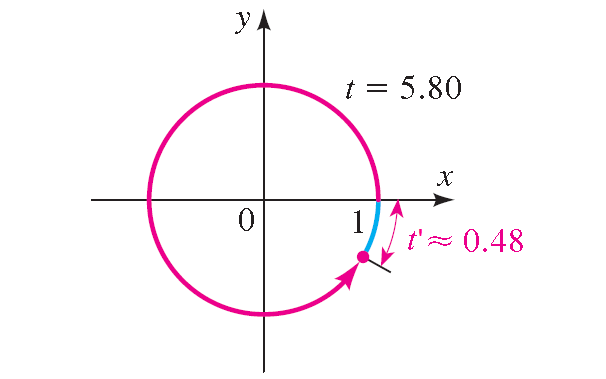
t' = 2π - 5.80 ≈ 0.48

17. Answer :

The reference numbers associated with these values of t were found in Problem 13.

The reference number is t' = π/6, which determines the terminal point (√3/2, 1/2) from the table.

Because the terminal point determined by t is in quadrant II, its x-coordinate is negative and its y-coordinate is positive. Thus, the desired terminal point is

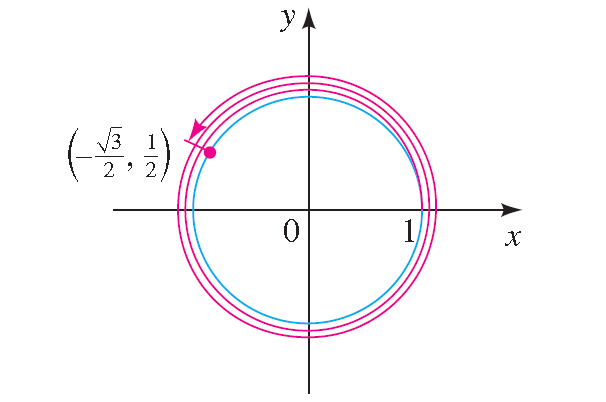
(-√3/2, 1/2)

18. Answer :

The reference numbers associated with these values of t were found in Problem 14.

The reference number is t' = π/4, which determines the terminal point (√2/2, √2/2) from the table.

Because the terminal point is in quadrant IV, its x-coordinate is positive and its y-coordinate is negative. Thus, the desired terminal point is

(√2/2, -√2/2)

19. Answer :

The reference numbers associated with these values of t were found in Problem 15.

The reference number is t' = π/3, which determines the terminal point (1/2, √3/2) from the table.

Because the terminal point determined by t is in quadrant III, its both x-coordinate and y-coordinate are negative. Thus, the desired terminal point is

(-1/2, -√3/2)

20. Answer :

Because

t = 29π/6 = 4π + 5π/6

we see that the terminal point of t is the same as that of 5π/6 (that is, we subtract 4π).

So by Example 13 the terminal point is

(-√3/2, 1/2)

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.