EXPONENTS AND LOGARITHMS WORKSHEET

Problem 1 : 

Solve for y :

3x² ⋅ 2x³ = 6x^y

Problem 2 :

If x² = y³ and x^3z = y⁹, then solve for z. 

Problem 3 :

Solve for x :

4^x - 3 ⋅ 2^x+2 + 2⁵ = 0

Problem 4 :

If 2^x = 3^y = 6^-z, then find the value of

¹⁄ₓ + ¹⁄y + ¹⁄z

Problem 5 :

Given that a^x = b^y = c^z and b² = ac. Solve for y in terms of x and z.

Problem 6 :

Solve for x :

log₂x - log₂5 = 2 + log₂3

Problem 7 :

If logx + logy = log(x + y), solve for y in terms of x.

Problem 8 :

Solve for x : 

(lnx)² - (ln2)(lnx) < 2(ln2)²

Problem 9 :

Solve for x :

log₂x + log₄x = log_0.25√6

Problem 10 :

Given that :

Find tghe value of p in terms of q. 

Answers

1. Answer :

3x² ⋅ 2x³ = 6x^y

(3 ⋅ 2)(x² ⋅ x³) = 6x^y

(6)(x²⁺³) = 6x^y

6x⁵ = 6x^y

Divide each side by 6. 

x⁵ = x^y

Using laws of exponents, we have

5 = y

2. Answer :

Given : x² = y³ and x^3z = y⁹.

x^3z = y⁹

x^3z = y^{3 ⋅ 3}

x^3z = (y³)³

Substitute y³ = x².

x^3z = (x²)³

x^3z = x⁶

3z = 6

Divide each side by 3.

z = 2

3. Answer :

4^x - 3 ⋅ 2^x+2 + 2⁵ = 0 

(2²)^x - 3 ⋅ 2^x ⋅ 2² + 32 = 0 

(2^x)² - 3 ⋅ 2^x ⋅ 4 + 32 = 0

(2^x)² - 12 ⋅ 2^x + 32 = 0

Let y = 2^x.

y² - 12y + 32 = 0

Solve by factoring.

y² - 8y - 4y + 32 = 0

y(y - 8) - 4(y - 8) = 0

(y - 8)(y - 4) = 0 

y - 8 = 0  or  y - 4 = 0 

y = 8  or  y = 4

Substitute 2^x for y.

2^x = 8  or  2^x = 4 

2^x = 2³  or  2^x = 2² 

x = 3  or  x = 2

4. Answer :

Let 2^x = 3^y = 6^-z = k.

Then we have

2^x = k ----> 2 = k^1/x

3^y = k ----> 3 = k^1/y

6^-z = k ----> 6 = k^-1/z

Now, we have

2 ⋅ 3 = 6

k^1/x ⋅ k^1/y = k^-1/z

Using laws of exponents, we have

k^{1/x + 1/y} = k^-1/z

¹⁄ₓ + ¹⁄y = -¹⁄z

Add ¹⁄z to both sides. 

¹⁄ₓ + ¹⁄y + ¹⁄z = 0

5. Answer :

Let a^x = b^y = c^z = k.

Then we have

b² = ac

a^x = k ----> a = k^1/x

b^y = k ----> b = k^1/y

c^z = k ----> c = k^1/z

Given : b² = ac.

(k^1/y)² = k^1/x ⋅ k^1/z

k^2/y ⋅ k^{1/x +1/z}

6. Answer :

log₂x - log₂5 = 2 + log₂3

log₂x - log₂5 = 2(1) + log₂3

log₂x - log₂5 = 2log₂2 + log₂3

log₂x - log₂5 = log₂2² + log₂3

log₂x - log₂5 = log₂4 + log₂3

Use the quotient rule and prule of logarithms.

log₂(ˣ⁄₅) = log₂(4 ⋅ 3)

log₂(ˣ⁄₅) = log₂(12)

If two logarithms are equal with the same base, then arguments can be equated.

ˣ⁄₅ = 12

Multiply each side by 5.

x = 60

7. Answer :

logx + logy = log(x + y)

Using the product rule of logarithms,

log(xy) = log(x + y)

xy = x + y

Subtract y from both sides.

xy - y = x

y(x - 1) = x

y = ˣ⁄₍ₓ ₋ ₁₎

8. Answer :

(lnx)² - (ln2)(lnx) < 2(ln2)²

Let y = lnx. 

y² - (ln2)y < 2(ln2)²

Subtract 2(ln2)2 from each side.

y² - (ln2)y - 2(ln2)² < 0

Factor.

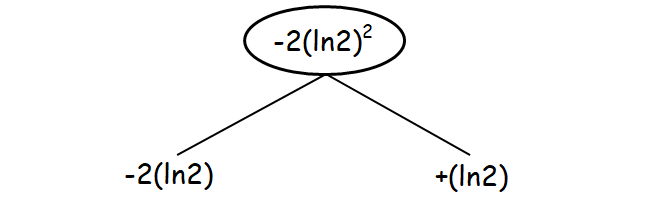
y² - 2(ln2)y + (ln2)y - 2(ln2)² < 0

y[y - 2(ln2)] + (ln2)[y - 2(ln2)] < 0

[y - 2(ln2)][y + (ln2)] < 0 ----(1)

Assume, [y - 2(ln2)][y + (ln2)] = 0 and solve for y.

[y - 2(ln2)][y + (ln2)] = 0

Mark -ln2 and 2(ln2) on the real number line.

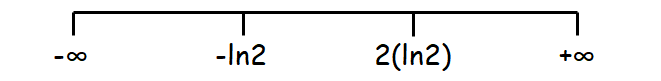
We can have the following intervals from the above real number line.

(-∞, -ln2), (-ln2, 2ln2), (2ln2, +∞)

In the above three intervals, only the interval (-ln2, 2ln2) satisfies the inequality (1).

-ln2 < y < 2ln2

Substitute lnx for y.

-ln2 < lnx < 2ln2

ln2^-1 < lnx < ln2²

ln(1/2) < lnx < ln4

1/2 < x < 4

9. Answer :

10. Answer :

Multiply both sides by 8.

p² + 4pq + 4q² = 8pq

Subtract 8pq from both sides.

p² - 4pq + 4q² = 0

p² - 2(p)(2q) + (2q)² = 0

(p - 2q)² = 0

p - 2q = 0

Add 2q to both sides.

p = 2q

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.