ROTATIONS
A rotation is a transformation in which a figure is turned about a fixed point. The fixed point is the center of rotation. Rays drawn from the center of rotation to a point and its image form an angle called the angle of rotation.
A rotation about a point A through x degrees (x°) is a transformation that maps every point B in the plane to a point B', so that the following properties are true.
1. If B is not point A, then
BA = B'A and ∠BAB' = x°
2. If B is point A, then
B = B'
Rotation can be clockwise or counterclockwise as shown below.
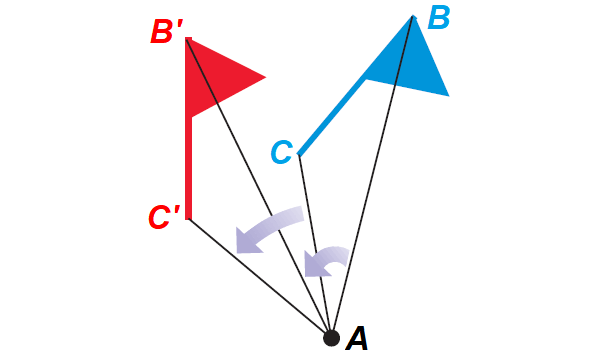
Clockwise Rotation of 90° :
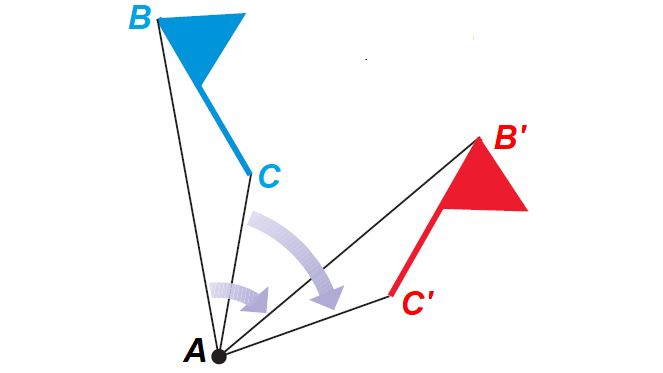
Counterclockwise Rotation of 90° :
Rotation Theorem
A rotation is an isometry.
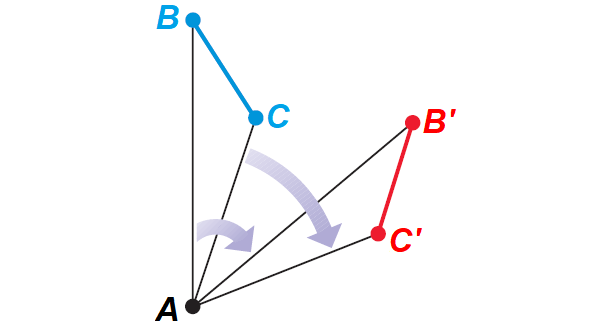
To prove the Rotation Theorem, we have to show that a rotation preserves the length of a segment. Consider a segment BC that is rotated about a point A to produce B'C'. The three cases to consider are shown below.
Case 1 :
C, B and A are noncollinear.
It has been illustrated in the diagram shown below.
Case 2 :
C, B and A are collinear.
It has been illustrated in the diagram shown below.
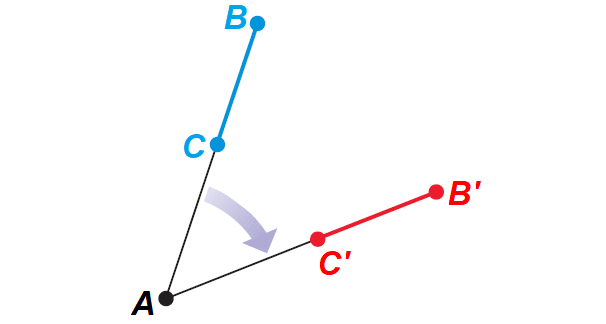
Case 3 :
A and C are the same point.
It has been illustrated in the diagram shown below.
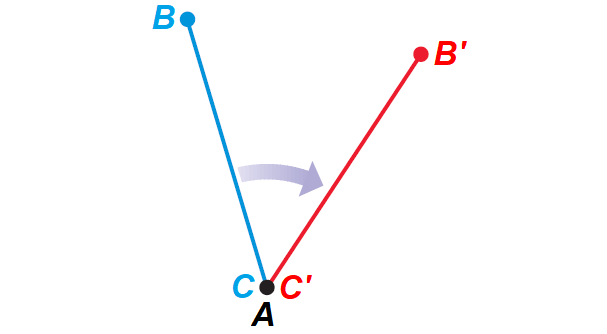
Proof of Case 1 of Rotation Theorem
Given : A rotation about A maps B onto B' and R onto R'.
Prove : BC ≅ B'C'
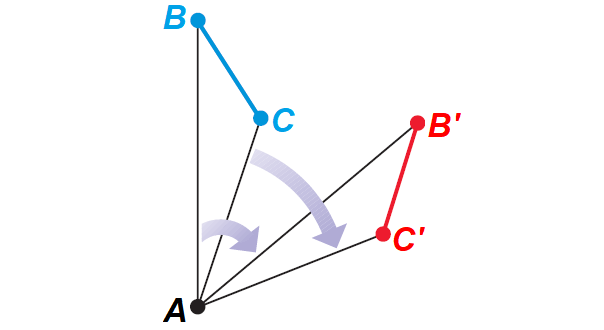
Proof :
By the definition of a rotation,
PQ = PQ' and PR = PR'
Also, by the definition of a rotation,
m∠BAB' = m∠CAC'
We can use the Angle Addition Postulate and the subtraction property of equality to conclude that
m∠BAC = m∠B'AC'
This allows us to use the SAS Congruence Postulate to conclude that
ΔBAC ≅ ΔB'AC'
Because corresponding parts of congruent triangles are congruent,
BC ≅ B'C'
using SAS Congruence Postulate.
Activity : Rotating a Figure
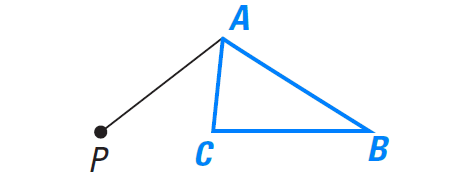
Use the following steps to draw the image of ΔABC after a 120° counterclockwise rotation about point P.
Step 1 :
Draw a segment connecting vertex A and the center of rotation point P.
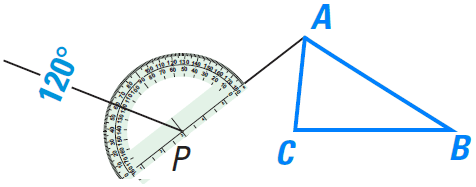
Step 2 :
Use a protractor to measure a 120° angle counterclockwise and draw a ray.
Step 3 :
Place the point of the compass at P and draw an arc from A to locate A'.
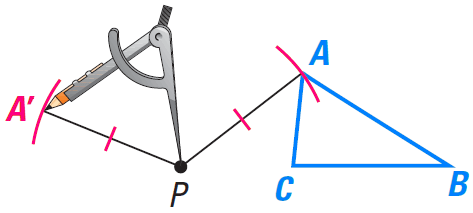
Step 4 :
Repeat steps 1-3 for each vertex. Connect the vertices to form the image.

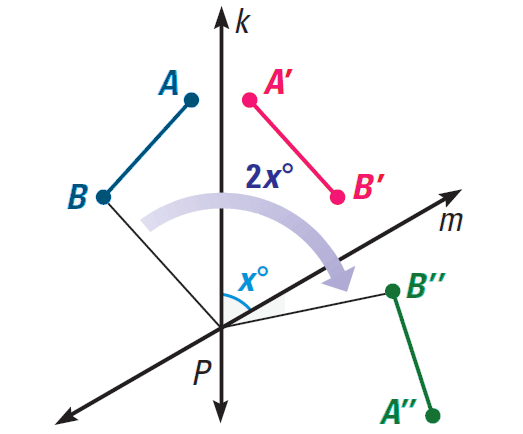
Rotation in Intersecting Lines - Theorem
If lines k and m intersecting at point P, then a reflection in k followed by a reflection in m is a rotation about point P.
In the diagram shown below, the angle of rotation is 2x°, where x° is the measure of the acute or right angle formed by k and m, then
∠BPB" = 2x°
Example :
In the diagram shown below, ΔRST is reflected in line k to produce ΔR'S'T'. This triangle is then reflected in line m to produce ΔR"S"T". Describe the transformation that maps ΔRST to R"S"T".
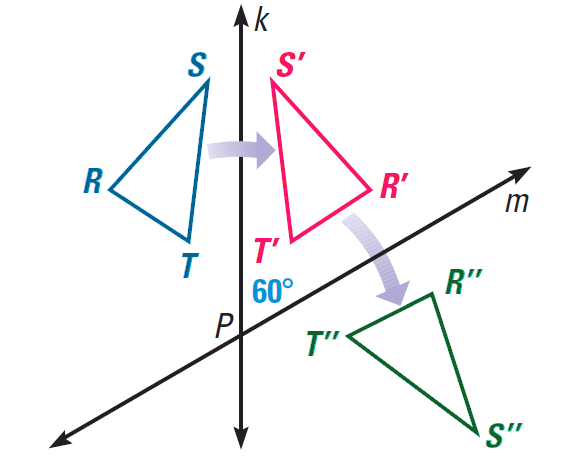
Solution :
The acute angle between lines k and m has a measure of 60°. Applying the above Theorem, we can conclude that the transformation that maps ΔRST to ΔR"S"T" is a clockwise rotation of 120° about point P.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Trigonometry Pythagorean Identities
May 02, 24 11:43 PM
Trigonometry Pythagorean Identities -
Trigonometry Quotient Identities
May 02, 24 11:08 PM
Trigonometry Quotient Identities -
Unit Rates
May 02, 24 09:27 AM
Unit Rates - Concept - Examples with step by step explanation